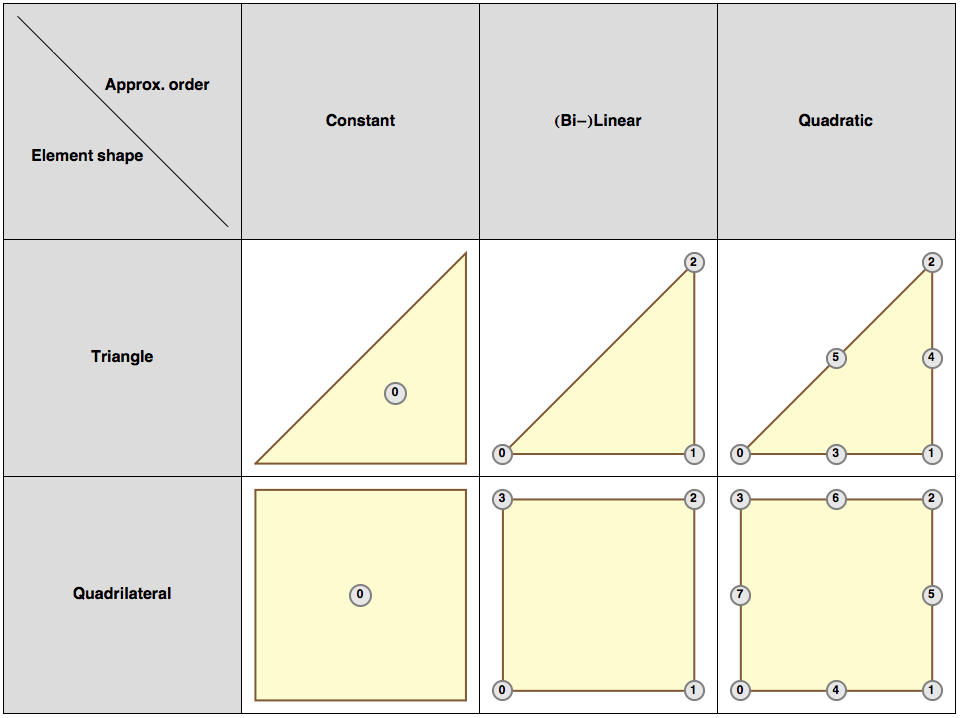
For the definition of the finite element space's basis the following information is needed:

Let's start from the back with the explanation of these items. Finite Element spaces are classified by categories or families of functions. These families subsume unique properties of the corresponding space. So far the BETL provides two fundamentally different families. The first one corresponds probably to the most common class of FE spaces. It is the family of Lagrangian or hat basis functions. These functions feature the well-known property

where ${\varphi }_i$ is the function corresponding to the $i\text{-th}$ local dof, ${\mathbf{p}}_j$ is the location of the $j\text{-th}$ local dof and ${\delta }_{ij}$ is the Kronecker symbol. Those functions are well suited for classical potential problems as well as for problems in acoustics. Another fundamental family is known as the family of edge functions. For instance, these functions are important for the discretisation of of Maxwell's equations. In BETL the Lagrangian functions are specified by the structure LagrangeTraits while the edge functions are either specified by EdgeDivTraits or by EdgeCurlTraits, respectively. Both, the EdgeDivTraits as well as the EdgeCurlTraits are edge functions. The only difference is that the latter contains the rotated functions of the former. Mathematically, this means that if $\mathbf{u}\in H\left(\text{div}{}_{\Gamma }\right)$ belongs to the space of functions where the surface divergence is square integrable, that $\mathbf{v}\in H\left(\text{curl}{}_{\Gamma }\right)$ belongs to the space of functions whose surface curls are square integrable. The connection between these functions is given by the rotation operator

such that $\mathbf{v}=\mathbf{R}\left(\mathbf{u}\right)$. In Equation 2.2 $\mathbf{n}$ is simply the outward normal vector.

The third item from the enumeration above describes how the degrees of freedom (dofs) will be distributed. For instance, a dof lying on an edge or on a corner of an element could be shared by all of its neighbouring elements or it may be exclusively attached to the current element. Within BETL, the first scenario is determined by the Continuous type and the second one is defined by the Discontinuous type. The decision whether the dofs might be distributed continuously or discontinuously might not be necessarily a property of the FEBasis. The decision is made herein because of the somehow famous “historical reasons”. The continuous/discontinuous dof distribution has been always a part of the FEBasis. That's it. Nevertheless, this may change in future versions of the BETL.

Let's go ahead. The second item from the enumeration describes the order of a function, i.e., whether the function might be constant, linear, quadratic, or of some higher order. For functions that belong to the Lagrangian family BETL implements constant, linear, and quadratic functions. Contrary, edge-functions are only implemented at lowest-order, i.e., currently only linear edge-functions are supported. The choice of the approximation order is made by the APPROX_ORDER enum.

The one item that is left is the first one from the enumeration. With this, one simply determines the general shape of an element, i.e., whether it is a triangle or a quadrilateral. Here, “general shape” means that the geometrical approximation of an element is by no means considered. Since the FEBasis is independent of any topological information it could be defined either on a flat or on a curved geometry approximation.

Now, since the description of the FEBasis is finished we can give some examples on how this data type is actually constructed.

#include "febasis/febasis.hpp"
using namespace betl;
// lowest order lagrangian functions on flat triangles
typedef FEBasis< Element<3>, 
                 CONSTANT, 
                 Discontinuous, 
                 LagrangeTraits > feb_e3_const_disc_lagr_t;
// lowest order divergence functions on flat triangles
typedef FEBasis< Element<3>, 
                 LINEAR, 
                 Continuous, 
                 EdgeDivTraits > feb_e3_lin_cont_div_t;
// quadratic, continuous functions on flat quadrilaterals
typedef FEBasis< Element<4>, 
                 QUADRATIC, 
                 Continuous, 
                 LagrangeTraits > feb_e4_quad_cont_lagr_t;
// linear, discontinuous functions on curved triangles
typedef FEBasis< Element<6>, 
                 LINEAR, 
                 Discontinuous, 
                 LagrangeTraits > feb_e6_lin_disc_lagr_t;

While Example 2.1, “Possible finite element basis declarations” depicts the possible choices for a finite element basis there exist also some combinations which are not allowed. Using these combinations within your code yields in rather crucial compiler errors.

#include "febasis/febasis.hpp"
using namespace betl;
// ERROR: a constant function can't be approximated continuously
typedef FEBasis< Element<3>, 
                 CONSTANT, 
                 Continuous, 
                 LagrangeTraits > feb_e3_const_cont_lagr_t;
// ERROR: constant edge functions do not exist
typedef FEBasis< Element<3>, 
                 CONSTANT, 
                 Discontinuous, 
                 EdgeCurlTraits > feb_e3_const_disc_curl_t;
// ERROR: higher order divergence functions are not implementd right now
typedef FEBasis< Element<3>, 
                 QUADRATIC, 
                 Continuous, 
                 EdgeDivTraits > feb_e3_quad_cont_div_t;
// ERROR: edge functions are only implemented for triangles
typedef FEBasis< Element<4>, 
                 LINEAR, 
                 Continuous, 
                 EdgeDivTraits > feb_e4_lin_cont_div_t;

Note that the first and second forbidden combinations in Example 2.2, “Impossible finite element basis declarations” are disallowed due to logical considerations while the two latter combinations are disallowed because of a lack of implementation. In future versions of BETL there might exist higher order edge functions and there might also exist edge functions for quadrilaterals.

Figure 2.1. Supported Lagrangian bases

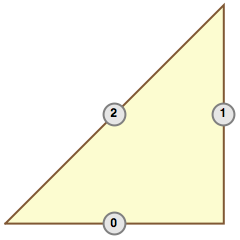
In Figure 2.1, “Supported Lagrangian bases”, the possible choices for Lagrangian based spaces as well as their local dof-numbering are depicted. Additionally, Figure 2.2, “Supported edge basis” shows the local dof distribution for the currently implemented edge bases.

Figure 2.2. Supported edge basis

For completeness, the following formula defines the lowest order edge functions for the $H\left(\text{div}{}_{\Gamma }\right)$ space

where $g_{\tau }$ denotes the Gram determinant of the element $\tau$ and ${\mathbf{p}}_{i\left(e\right)}$ is the triangle's $i\text{-th}$ vertex lying opposite to the edge $e$ .

Once the FEBasis has been defined the creation of the finite element space is a quite easy task. As it has been already said at the beginning of this section the finite element space is spanned by an object called DoFHandler. This data type combines the bases of the finite element space with the topological information. The following example illustrates the declaration and instantiation of the DoFHandler

#include "febasis/febasis.hpp"
#include "dof_handler/dof_handler.hpp"
using namespace betl;
// lowest order lagrangian functions on flat triangles
typedef FEBasis< Element<3>, 
                 CONSTANT, 
                 Discontinuous, 
                 LagrangeTraits > feb_e3_const_disc_lagr_t;
// declare the dof handler data type
typedef DoFHandler< feb_e3_const_disc_lagr_t > dofhandler_t;
// instantiate the dofhandler
dofhandler_t dofhandler;
// span the finite element space
dofhandler.distributeDoFs( mesh.e_begin(), mesh.e_end() );

In Example 2.3, “A possible dof handler declaration” the mesh object has not been declared but one might deduce that this variable represents the mesh on which the analysis will take place. Moreover, the creation of the finite element space's basis has been directly taken from Example 2.1, “Possible finite element basis declarations”. As you see the creation of the finite element step involves three steps:

Please refer to the section called “Example 2: The DofHandler concept” for an example about the usage of the dof handler.