Proseminar:
Hierarchische
Matrizen
Vorträge:
- Ein Einfuehrungsbeispiel [7, Sect. 1],
Herr Mirko Baechtiger, 16.4.2004 SlidesI, SlidesII
- Mehrdimensionale Clusterbäume [7,
Sect. 2.1], Herr Jean-Marie Droz,
16.4.2004, Slides
- Mehrdimensionale Block-Clusterbäume [7,
Sect. 2.2], Herr Roman Jud,
30.4.2004, Slides
- Mehrdimensionale Interpolation [7,
Sect. 3.2], Herr Aniello Esposito,
30.4.2004, Slides
- Randintegralgleichungen [7, Sect. 3.1
& 3.3], Herr Christian Perret,
7.5.2004, Slides I, Slides II
- H-Matrizen und elliptische Randwertprobleme [7,
Sect. 4], Herr Lukas Wampfler,
7.5.2004, Slides
- H-Matrix-Arithmetik: Niedrigrangmatrizen (Komplexität) [7,Sect. 5.1] und [7,
Sect. 6.1], see also [7], Herr Raphael Scheiwiller, 28.5.2004, Slides
- H-Matrix-Arithmetik: Addition (Komplexität)[7,
Sect. 5.2] und [7,Sect. 6.2], see also [7], Herr Michael
Graenz, 28.5.2004, Slides
- H-Matrix-Arithmetik: Multiplikation [7,
Sect. 5.2], see also [7], Herr Remo Crameri, 4.6.2004, Slides
- H-Matrix-Arithmetik: Multiplikation - Komplexitaet [7, Sect. 6.2.3], see also [7],
Herr Jean-Marie Droz, 4.6.2004, Slides
- H-Matrix-Arithmetik: Inversion (Komplexität) [7,
Sect. 5.2.2] und [7,
Sect. 6.2.4], see also [7], Herr Anielli
Esposito, 11.6.2004, Slides
- H-Matrix-Arithmetik: LU-Zerlegung [7 Sect
5.2.3.], Herr Remo Crameri, 11.6.2004, Slides
- ACA I [3, Sect. 1-3.2], Herr Christian Perret, 18.6.2004, Slides
- ACA II: Fehlerabschaetzungen [3,
Sect. 3.3 & 3.4], Herr Roman
Jud, 18.6.2004, Slides
- Eigenschaften der Blockclusterbaeume [7,
Sect. 6.3], Herr Lukas Wampfler,
25.6.2004
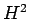 -Matrizen: Motivation [7,
Sect. 8.1], Herr Mirko Baechtiger,
25.6.2004
-Matrizen: Motivation [7,
Sect. 8.1], Herr Mirko Baechtiger,
25.6.2004
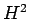 -Matrizen: Definition [7,
Sect. 8.2], Herr Raphael
Scheiwiller, 2.7.2004
-Matrizen: Definition [7,
Sect. 8.2], Herr Raphael
Scheiwiller, 2.7.2004
- Adaptive Clusterbasen [7, Sect. 8.3],
Herr Michael Graenz, 2.7.2004
- The Fast Multipole Method (FMM) I: [1,
Sect. 1-2], -
- The Fast Multipole Method (FMM) II: [1,
Sect. 3-4], -
- FMM in 3D [1, Sect. 5], -
- FMM for wave propagation [9a], -
Viele Vorträge sind algorithmisch orientiert, wobei in der
zugrundeliegenden
Literatur auf ein C-Bibliothek (HLIB) vom MPI Leipzig Bezug genommen
wird. Diese
Bibliothek steht zur Verfügung (Download)
und kann bei der Vorbereitung der Vorträge eingesetzt werden.
| Dozenten |
: |
Prof. R. Hiptmair |
| Ort |
: |
HG E 22 |
| Zeit |
: |
Fr 10:15-12:00 |
| beginnt am |
: |
16.4.2004 |
| Vorbesprechung |
: |
Fr 2.4.2004, 10:15, HG
E 22 |
| Kontaktperson |
: |
R. Hiptmair,
hiptmair@sam.math.ethz.ch |
| HLIB-Beratung |
: |
K. Schmidt,
kersten.schmidt@sam.math.ethz.ch |
| Voraussetzungen |
: |
Solide Kenntnisse in
Linearer Algebra (Matrizenrechnung),
Grundkenntnisse in Analysis. Vetrautheit mit einer Programmiersprache
(C, C++ oder
JAVA) |
Beschreibung:
Im Rahmen numerischer Simulationen von Vorgängen in
Naturwissenschaft
und Technik treten oft lineare Gleichungssysteme mit grossen
vollbesetzten Matrizen auf. Im allgemeinen Fall einer vollbesetzten n x
n -Matrix benötigt
die Multiplikation mit einem Vektor quadratischen Aufwand in n, die
Lösung
eines Gleichungssystems mit Gausselimination sogar kubischen Aufwand.
Nun hat man bemerkt, dass viele dieser Matrizen eine verborgene
Struktur
aufweisen, da sie mit Integraloperatoren mit schnell abfallenden Kernen
in Beziehung stehen. Dies lëst sich dadurch ausnutzen, dass man
eine
gute Näherung der Matrix durch lokale Niedrigrangapproximation
erhalten
kann. Das resultierende Speicherformat ist bekannt als "Hierarchische
Matrix"
(H-Matrix).
Gegenstand des Seminars ist dieses hierarchische Matrixformat und
darauf
aufbauende Algorithmen zur Multiplikation Matrix-Vektor, zur
approximativen
Matrixmultiplikation und Invertierung. Diskutiert werden die
mathemtischen
Grundlagen, die Details der Algorithmen und deren Komplexität.
Die Idee der hierarchischen Matrizen stellt eine bedeutende
Innovation
der modernen numerischen Mathematik dar. Sie steht in enger Beziehung
zu den sogenannten Fast-Multipole-Verfahren fuer nichtlokale Operatoren
und zum Panel-Clustering fuer Randelementgleichungen. Ihr Potential
ist noch lange nicht ausgeschöpft.
Die Vortraege im Seminar werden sich im wesentlichen auf ein
Skriptum "Hierarchical Matrices" (S. Boerm, L. Grasedyck, W. Hackbusch,
Max-Planck Institut fuer Mathematik in den Naturwissenschaften,
Leipzig)
stützen. Daneben werden noch einige ausgewählte Publikationen
herangezogen.
Allgemeines zu den Präsentationen
- Jeder Teilnehmer hat zwei
Vorträge von jeweils maximal 45 Minuten
dauer zu halten.
- Die zur Praesentation verwendeten Medien muessen den anderen
Seminarteilnehmern in elektronischer Form (PDF) zur Verfuegung gestellt
werden. Im Falle eines (teilweisen) Tafelvortrages ist eine
Ausarbeitung
zu den betreffenden Passagen anzufertigen.
- Für die Präsentationen steht ein Laptop mit Acrobat
Viewer zur
Verfuegung.
Der Beamer muss vor dem
Vortrag im HG D 26.2 vom Vortragenden abgeholt werden und ist bis
15:30 dort wieder abzugeben.
Die meisten relevanten Publikationen sind in elektronischer Form
verfuegbar (Download)
-
- 1
BEG97:
- R. BEATSON AND L. GREENGARD,
A short course on fast multipole methods, in Wavelets,
Multilevel Methods and Elliptic PDEs, M. Ainsworth,
K. Levesley, M. Marletta, and W. Light, eds., Numerical
Mathematics and Scientific Computation, Clarendon Press, Oxford, 1997,
pp. 1-38.
- 2
BEH03:
- M. BEBENDORF AND W. HACKBUSCH,
Existence of
 -matrix approximants
to the inverse FE-matrix of elliptic operators with
-matrix approximants
to the inverse FE-matrix of elliptic operators with  -coefficients,
Numerische Mathematik, 95 (2003), pp. 1-28.
-coefficients,
Numerische Mathematik, 95 (2003), pp. 1-28.
- 3
BER03:
- M. BEBENDORF AND S. RJASANOV,
Adaptive low-rank approximation of collocation matrices,
Computing, 70 (2003), pp. 1-24.
- 4
BOE03:
- S. BÖRM,
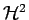 -matrices -- multilevel methods for the
approximation of integral operators, Tech. Report 7, Max
Planck Institute for Mathematics in the Sciences, 2003.
-matrices -- multilevel methods for the
approximation of integral operators, Tech. Report 7, Max
Planck Institute for Mathematics in the Sciences, 2003.
To appear in Computing and Visualization in the Sciences.
- 5
BOG02:
- S. BÖRM AND L. GRASEDYCK,
Low-rank approximation of integral operators by interpolation,
Tech. Report 72, Max Planck Institute for Mathematics in the
Sciences, 2002.
To appear in Computing.
- 6
BGH03:
- S. B¨ORM, L. GRASEDYCK, AND W. HACKBUSCH,
Introduction to hierarchical matrices with applications,
Engineering Analysis with Boundary Elements, 27 (2003),
pp. 405-422.
- 7
BGH03b:
- S. B¨ORM, L. GRASEDYK, AND W. HACKBUSCH,
Hierarchical matrices, Lecture notes 21, MPI für
Mathematik in den Naturwissenschaften, Leipzig, Germany, 2003.
- 8
BOH01:
- S. BÖRM AND W. HACKBUSCH,
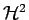 -matrix
approximation of integral operators by interpolation, Applied
Numerical Mathematics, 43 (2002), pp. 129-143.
-matrix
approximation of integral operators by interpolation, Applied
Numerical Mathematics, 43 (2002), pp. 129-143.
- 9
BOH03:
- S. BÖRM AND W. HACKBUSCH,
Approximation of boundary element operators by adaptive
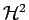 -matrices, Tech. Report 5, Max Planck
Institute for Mathematics in the Sciences, 2003.
-matrices, Tech. Report 5, Max Planck
Institute for Mathematics in the Sciences, 2003.
To appear in Foundations of Computational Mathematics.
- 9a CRW93a:
- R. Coifman, V.Rokhlin and S. Wandzura, The fast multipole
method for the wave equation: A pedestrian approach, IEEE Antennas
and Propagation Magazine, 35(3), 1993
- 10
GHK02:
- I. GAVRILYUK, W. HACKBUSCH, AND B. KHOROMSKIJ,
Data-sparse approximation to operator-valued functions of
elliptic operator, Tech. Report 54, Max Planck Institute for
Mathematics in the Sciences, 2002.
To appear in Mathematics of Computation.
- 11
GHK02a:
- I. GAVRILYUK, W. HACKBUSCH, AND B. KHOROMSKIJ,
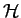 -matrix approximation for the
operator exponential with applications, Numerische Mathematik, 92
(2002), pp. 83-111.
-matrix approximation for the
operator exponential with applications, Numerische Mathematik, 92
(2002), pp. 83-111.
- 12
GHK03:
- I. GAVRILYUK, W. HACKBUSCH, AND B. KHOROMSKIJ,
Data-sparse approximation of a class of operator-valued
functions, Tech. Report 20, Max Planck Institute for
Mathematics in the Sciences, 2003.
To appear in Mathematics of Computation.
- 13
GRA0:
- L. GRASEDYCK, Theorie und Anwendung
Hierarchischer Matrizen, phd thesis, Universität Kiel, Kiel,
Germany, 2001.
- 14
GRH03:
- L. GRASEDYCK AND W. HACKBUSCH,
Construction and arithmetics of
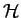 -matrices,
Computing, 70 (2003), pp. 295-334.
-matrices,
Computing, 70 (2003), pp. 295-334.
- 15
GHL01:
- L. GRASEDYCK, W. HACKBUSCH, AND S. LEBORNE,
Adaptive refinement and clustering of
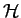 -matrices, Tech. Report 106, Max Planck
Institute of Mathematics in the Sciences, 2001.
-matrices, Tech. Report 106, Max Planck
Institute of Mathematics in the Sciences, 2001.
- 16
HAC99:
- W. HACKBUSCH, A sparse matrix arithmetic
based on
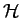 -matrices. Part I: Introduction to
-matrices. Part I: Introduction to 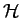 -matrices, Computing, 62 (1999),
pp. 89-108.
-matrices, Computing, 62 (1999),
pp. 89-108.
- 17
HAB02:
- W. HACKBUSCH AND S. B¨ORM,
Data-sparse approximation by adaptive
 -matrices,
Computing, 69 (2002), pp. 1-35.
-matrices,
Computing, 69 (2002), pp. 1-35.
- 18
HAK00:
- W. HACKBUSCH AND B. KHOROMSKIJ,
A sparse
 -matrix arithmetic: General
complexity estimates, J. Comp. Appl. Math., 125 (2000),
pp. 479-501.
-matrix arithmetic: General
complexity estimates, J. Comp. Appl. Math., 125 (2000),
pp. 479-501.
Prof. Ralf
Hiptmair
2004-02-16